A Way to remember the Entire Unit Circle for Trigonometry

Okay. I did a video about the unit circle. I just filled in the top right quadrant. People have asked me to do the rest of it so I guess here we go.

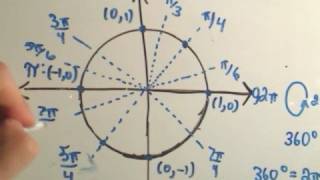
Here's a way to remember the unit circle. There are a couple of tricks to at least help you along the way. Again the unit circle is a circle that has a radius 1 so this is 1, 0.  In this video, I am going to label the entire unit circle.

The unit circle is simply a circle of radius one, so we
can easily plot points: (1,0) , (0,1) , (-1,0) (0,-1). The circumference of a circle is C = 2 * pi * r and
since our circle has radius 1, the circumference is C = 2pi. We measure angles from the positive x axis
and positive angles in a counter-clockwise direction. So if we start at the positive X-axis and travel the
entire distance around the circle, we have traveled 2pi radians.

So if we travel half of the distance around
the circle, we have traveled pi radians. So if we travel pi radians, we are at the point (-1,0) at the top of the circle, we would be at pi / 2
radians and at the bottom we would be at 3pi/2 radians. If we divide the first quadrant into two pieces, we have traveled one half
of pi/2 so we will be at an angle of pi / 4 We can now count one pi / 4 , 2pi/4 will put us at the top of the circle, 3pi / 4 will be in quadrant
2, 4pi/4 will be along the negative X-axis, 5pi/4 will place us in the middle of quadrant 3, 6pi/4 is the bottom of the circle And 7pi / 4 will put in the middle of quadrant 4. We can now do the same thing with the angle pi/6 (or 30
degrees) and begin counting off multiples of pi/6 to find more angles.

60 Degrees, or 2pi/6 = pi/3  will be in between pi/4 and pi/2. If we subtract the angle pi/6 from 1pi,
we are left with the angle 5pi/6 If we travel a little below the negative X-axis by adding the
angle pi/6 we will then be at the angle 7pi/6. If we travel all the way around, we will be at 12pi/6 = 2pi, so
if we subtract the angle pi/6 we will be at the angle 11pi/6. Next we can add the angle 2pi/3 =
120 degrees which is in quadrant 2.

The angle 3pi/3 is along the negative X-axis, so if we add pi/3
to that angle, we get 4pi/3 which is in quadrant 3. Lastly if we subtract pi/3 from 6pi/3 = 2pi, we get
the angle 5pi/3 , which is in quadrant 4. Now we have to fill in the values that corresponds
to points on the circle for a given angle. The way that you can remember the points is to start by
making fractions and making each fraction have a denominator of 2.

Now write: 1, 2, 3 as the numerator of each of
the first coordinates, writing from the top to the bottom Then we write 1, 2, 3 as the numerators of
the second coordinates starting from the bottom point And then we simply take the square root of each number in the numerator. Now we begin finding the other values simply by reflecting points
and changing signs ( + / - ) where necessary. In this case, the x coordinates will now
all become negative in the second quadrant Likewise, in the 3rd quadrant, both coordinates are negative while
in quadrant 4, only the y-coordinate is negative. (Now I proceed to label the rest of the points
using the methods I just described: reflection and changing signs) And now we have labeled the unit circle!
 I hope this method helps you!.